Can lattice cryptography quantum-proof blockchains?
How lattice cryptography can protect blockchains from quantum computing and the potential challenges of implementation
In my previous article, I explained how current popular cryptography algorithms, such as the Elliptic Curve Digital Signature Algorithm (ECDSA), will become insecure with the advent of advanced quantum computing, a type of computer that will be more powerful than all computers on Earth combined. The immediate effects include hackers stealing users’ cryptocurrency funds and making unauthorized transactions on blockchains, as well as numerous large-scale problems outside of blockchains.
Researchers are developing post-quantum cryptography, which involves new cryptographic algorithms and encryption methods designed to resist the power of quantum computing and remain secure as it advances.
One of the most promising post-quantum cryptography methods is lattice cryptography, a type of cryptography based on complex, multi-dimensional lattices, unlike elliptic curves, which ECDSA relies on. Several major blockchains, such as Algorand and Linea, are exploring the use of lattice cryptography, while many researchers suggest theoretical ways to integrate it into blockchain architecture.
This article describes the foundation of lattice cryptography, its potential to resist quantum computing, and outlines research in implementing it into blockchain technology.
How lattice cryptography is more secure
Lattice cryptography is based on mathematical problems that are more difficult to solve, making them more secure than elliptic curve cryptography and other cryptographic methods. Computer systems must overcome much more geometric and spatial complexities to break lattice cryptography.
The geometric foundation of lattice cryptography
Lattice cryptography features a more complex geometric structure with greater space and unpredictability than elliptic curves.
Lattice cryptography is based on lattices, infinite sets of regularly spaced points in space. Many vectors, which are lines with a direction and length, can exist in a lattice.
Consider two-dimensional lattices as never-ending graph paper that allows you to draw points and arrows.

Consider three-dimensional lattices as never-ending isometric graph paper that allows you to draw three-dimensional objects.
Multi-dimensional lattices, which are difficult for the human eye to visualize, enable objects with infinite dimensions.
Elliptic curve cryptography is based on elliptic curves, which are smooth, cubic curves defined by algebraic formulas or equations. Unlike lattices, elliptic curves are more accurately defined and predictable based on the algebraic formulas associated with them.
Although not a direct comparison, elliptic curve cryptography is similar to trying to get a perfect score in a 2D game multiple times. Imagine collecting all the possible coins in Mario Kart in hundreds of games. It is challenging to accomplish, but in theory, it is possible.

Consider trying to break lattice cryptography as attempting to complete a never-ending game where an endless stream of scenes and dialogues is constantly generated by artificial intelligence. It is still possible, but much harder to do.
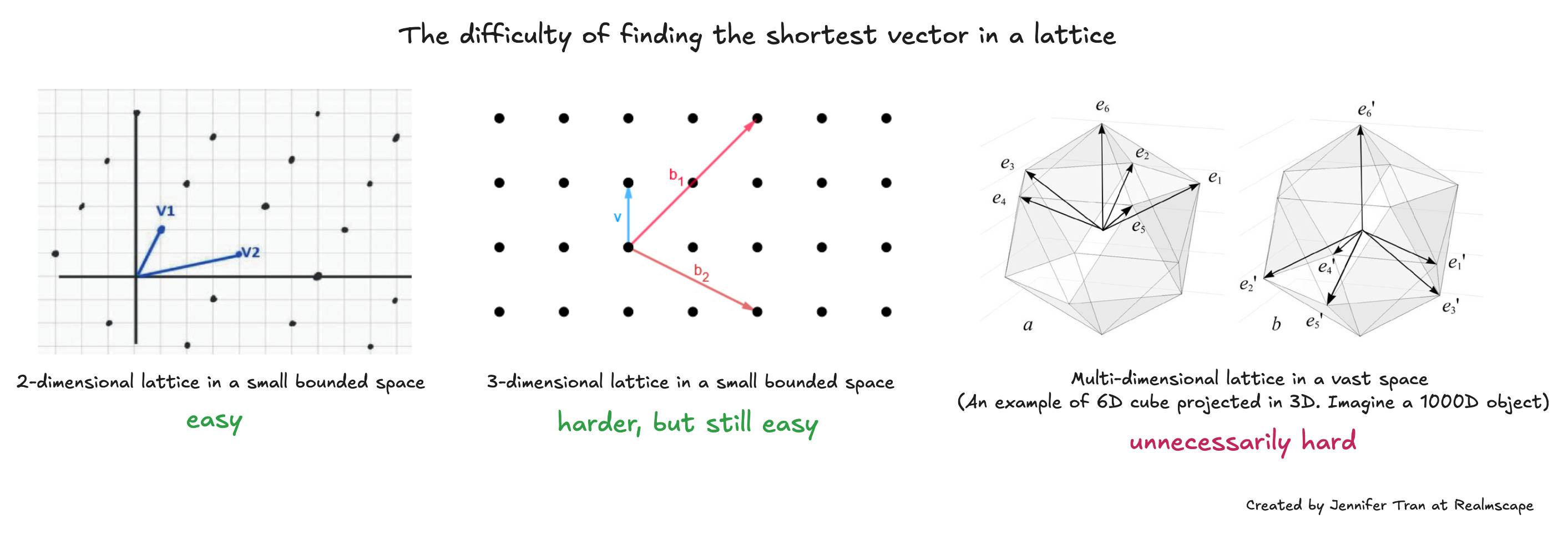
The more complex geometric structure underlying lattice cryptography leads to more challenging mathematical problems that a computer system must solve to verify lattice cryptography.
Breaking lattice cryptography
Quantum computers are currently unable to identify all the possibilities required to completely break lattice cryptography.
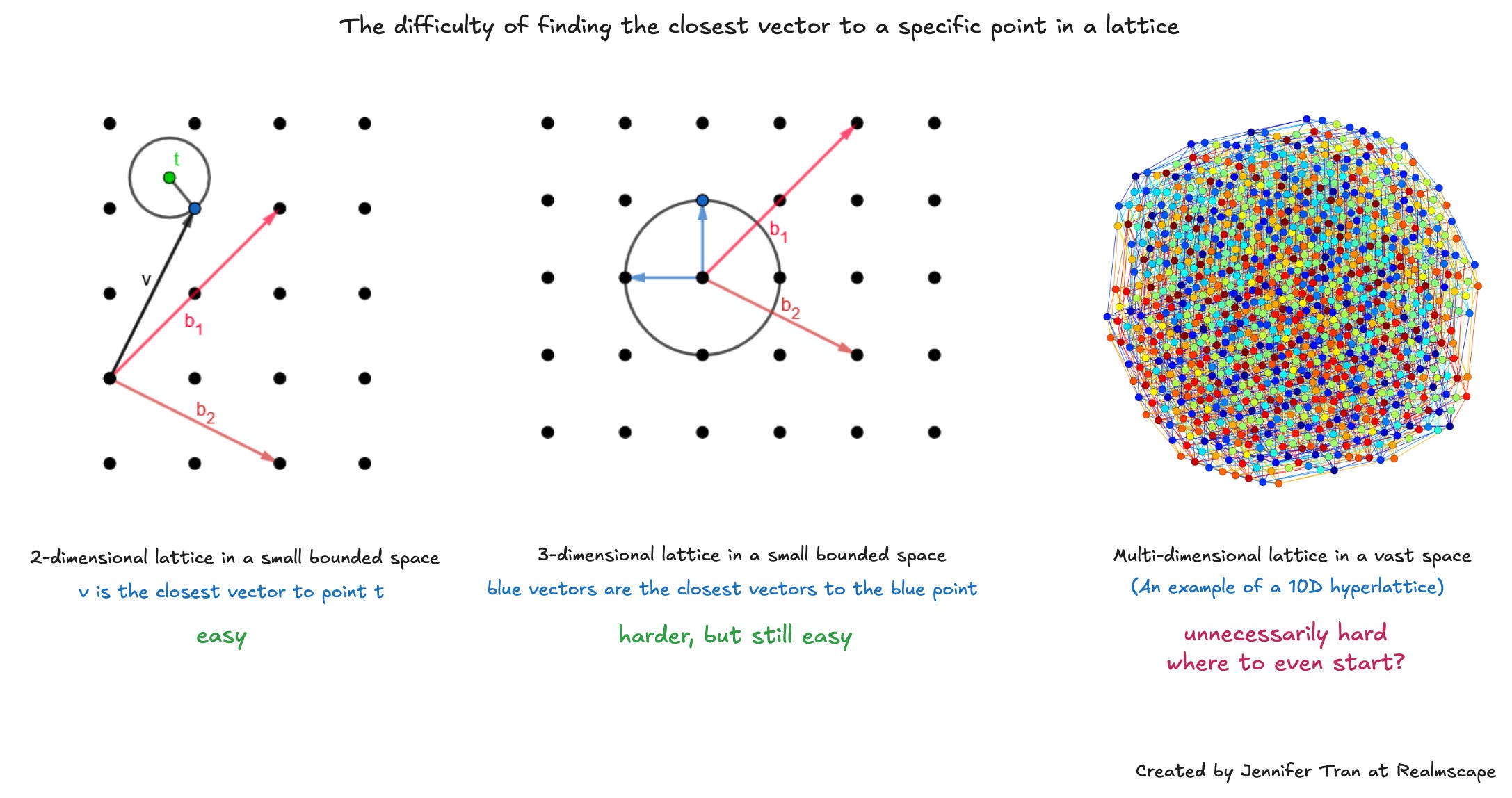
To fully break lattice cryptography, a computer system would need to find the shortest and closest vectors relative to a given point in the lattice, which no quantum computer can currently perform quickly enough to be practical.
Finding the shortest vector is simple in two or three dimensions, but becomes difficult even for a quantum computer in thousands or even infinite dimensions.
Finding the closest vector to a given point in a lattice, when many vectors exist in infinite dimensions, is also impossible [1].
The geometric and spatial vastness of lattice cryptography requires even more specialized computing than current quantum computing to break it. An advanced algorithm or computer system in the future might break lattice cryptography, but for now, we are safe.
Applications of lattice cryptography in blockchain
Lattice cryptography clearly meets security standards. It also needs to be fast and size-efficient enough to run on a classical computer for it to be practical for blockchain implementation.
Several major blockchains, such as Algorand and Linea, have found lattice cryptography reasonably practical and are implementing it for specific use cases. For example, Linea, an Ethereum-compatible Layer 2 blockchain scaling solution that uses zero-knowledge proofs (also known as a zkEVM), hashes data with a lattice-based function in its prover. A prover generates proofs that confirm the validity of computations or transactions [6].
At the same time, many researchers propose theoretical approaches to integrate it into blockchain architecture, while still questioning their practicality.
The following section examines research conducted by various blockchain teams on the advantages and disadvantages of FALCON signatures, a lattice-based cryptographic algorithm.
Using FALCON signatures
Fast Fourier lattice-based compact signatures (FALCON), a lattice cryptography method designed for compactness, is currently the most widely implemented and researched within the blockchain space.
Blockchain users sign transactions from their wallets using a cryptographic algorithm, such as ECDSA, generating a signature. Then, nodes or software that connect to the blockchain use this signature to verify that the user authorized the transaction.
Current research, including from Algorand, Manta Network, Sui, and Ethereum, focuses on utilizing FALCON as the primary cryptographic algorithm to generate these signatures.
The benefits of using FALCON
Researchers state that FALCON’s rapid speed, small size, and compatibility with current computers make it attractive for implementation.
The generation of FALCON signatures is relatively fast, although the speed varies depending on the specific use case. In general, FALCON signatures are generated three times faster than traditional cryptography algorithms, but are 1.6 to 1.8 times slower to verify.
Several blockchains, such as Cardano and Polkadot, select their block creators by generating random numbers using a verifiable random function (VRF) and signing the result to confirm its authenticity. Researchers from Manta Network, an Ethereum-compatible Layer 2 scaling solution that utilizes modular components to process transactions on its chain, discovered that signing results from a custom-made VRF using FALCON signatures were sufficiently fast, though slower than traditional Elliptic Curve Cryptography and Rainbow, another post-quantum signature scheme. For example, 624 transactions signed using the custom-made VRF results with Falcon signatures on a 10-node blockchain within one second, compared to 353 signed with Dilithium (a post-quantum signature scheme), 997 with Rainbow, and 1,000 with Elliptic Curve Cryptography [7].
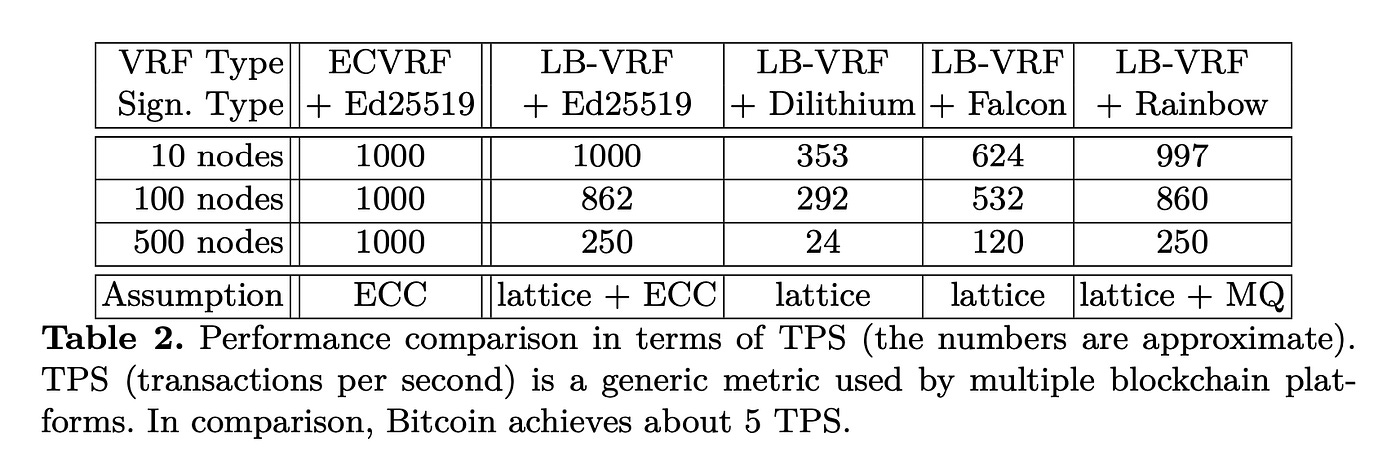
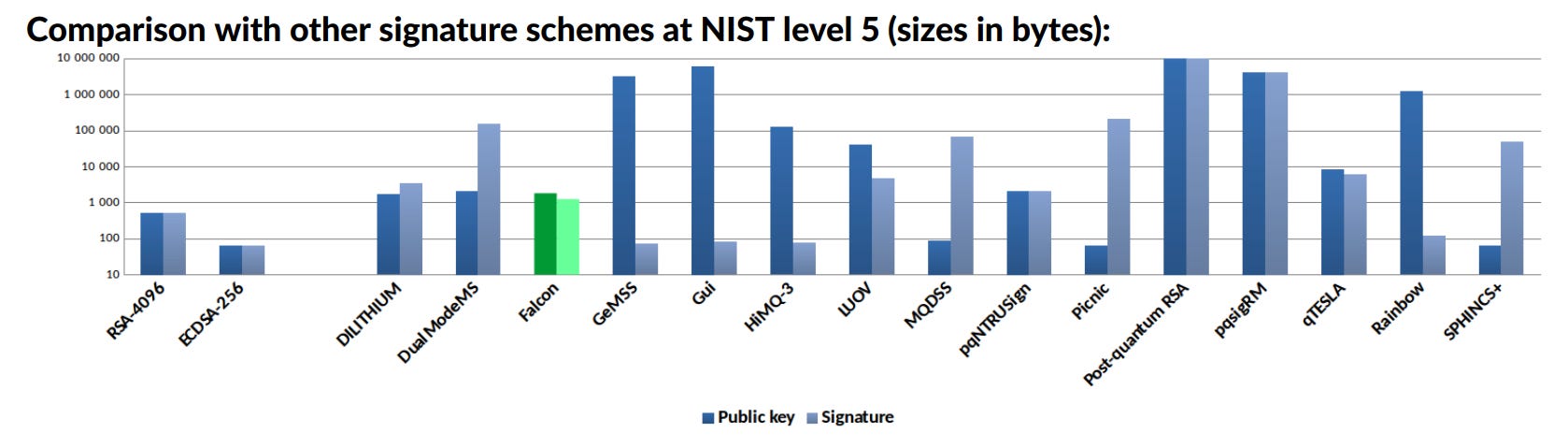
FALCON public keys and signatures are generally more compact than those of other post-quantum cryptography algorithms, which may have small signatures but significantly larger public keys or vice versa. Key and signature generation and verification occur within milliseconds on small computers, allowing users to continue using their mobile phones and laptops to interact with the blockchain.
The worst-case running time, or the maximum time it takes to execute as the problem size increases, grows only slightly faster than the chosen lattice dimension input. In other words, the algorithm scales gracefully as you select a higher-dimensional lattice on which the cryptographic problems are based [5].
Clearly defined computing expectations are beneficial for blockchains that require consistent performance, and execution times are crucial for scalability and reliability [4].
The benefits are sufficient for some researchers and developers to advocate for integrating FALCON into specific blockchains.
Ethereum developers are pushing for a FALCON signature verifier to be integrated into the protocol.
Algorand, a Layer 1 blockchain based on pure proof-of-stake, has incorporated FALCON signatures into their state history workflow in production, citing its size, compactness, and compatibility with classic computers.
On Algorand, nodes generate a set of FALCON public-private key pairs that can be used to create FALCON signatures.
func GenerateFalconSigner(seed FalconSeed) (FalconSigner, error) {
pk, sk, err := cfalcon.GenerateKey(seed[:])
return FalconSigner{
PublicKey: FalconPublicKey(pk),
PrivateKey: FalconPrivateKey(sk),
}, err
}Upon creating new transaction blocks, they use these keys to sign and verify state proofs, which act as a snapshot of the current state of the Algorand chain at a specific moment [3].
func (d *FalconSigner) Sign(message Hashable) (FalconSignature, error) {
hs := Hash(HashRep(message))
return d.SignBytes(hs[:])
}To review the complete code for the FALCON public-private key generation process for Algorand nodes, please refer to the following resources:
Changelog, which includes descriptions of code changes
The pull request containing the code updates
The complete FALCON code implementation that the Algorand SDK calls to
The downsides of using FALCON
In addition to the slower verification times, researchers note that FALCON is challenging to implement and requires floating-point arithmetic, a type of math that utilizes real numbers, which has several limitations.
Sui, a Layer 1 blockchain that processes transactions concurrently, found FALCON limiting due to its inability to verify signatures in batches. The lattice-based design makes it challenging to perform batch verifications using traditional algebraic methods in standard cryptographic algorithms.
Researchers on Ethereum have suggested that the limitations of floating-point arithmetic, such as a computer’s binary representation being unable to handle decimal numbers, will add complexity to a full implementation on Ethereum. Floating-point arithmetic can also cause security issues by unintentionally leaking information [5].
Conclusion
Lattice cryptography within blockchain systems currently shows promise, as evidenced by recent research and early implementations from several blockchains.
Although predicting the near future is challenging, lattice cryptography is currently secure against quantum computing due to its geometric and spatial complexities. Lattice cryptography is also fast, compact, and compatible with current computer systems, making it practical for blockchain researchers to consider implementing.
FALCON signatures are the most extensively researched and widely used, with Algorand leading in production-based implementation. Linea uses lattice-based hash functions, while Ethereum, Sui, and Manta Network are actively and publicly exploring lattice-based cryptography.
Sources
[1] The Mathematical Foundation of Post-Quantum Cryptography, https://spj.science.org/doi/full/10.34133/research.0801
[2] FALCON, https://csrc.nist.gov/CSRC/media/Presentations/Falcon/images-media/Falcon-April2018.pdf
[3] Algorand State Proofs Overview, https://developer.algorand.org/docs/get-details/stateproofs/
[4] Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU, https://falcon-sign.info/falcon.pdf
[5] Falcon as an Ethereum transaction signature: the good, bad, and the gnarly, https://ethresear.ch/t/falcon-as-an-ethereum-transaction-signature-the-good-the-bad-and-the-gnarly/21512
[6] Linea Prover Documentation, https://eprint.iacr.org/2022/1633.pdf
[7] Practical Post-Quantum Few-Time Verifiable Random Function with Applications to Algorand, https://eprint.iacr.org/2020/1222.pdf



