Why is ECDSA not quantum-resistant?
How ECDSA, the most popular cryptographic algorithm that powers many blockchains, becomes insecure if advanced quantum computing becomes a reality
This article outlines current concerns that quantum computing could compromise the core cryptography underlying blockchains, explaining how the Elliptic Curve Digital Signature Algorithm (ECDSA) works and why it would become insecure in the presence of quantum computing.
Current Concerns of Top Researchers
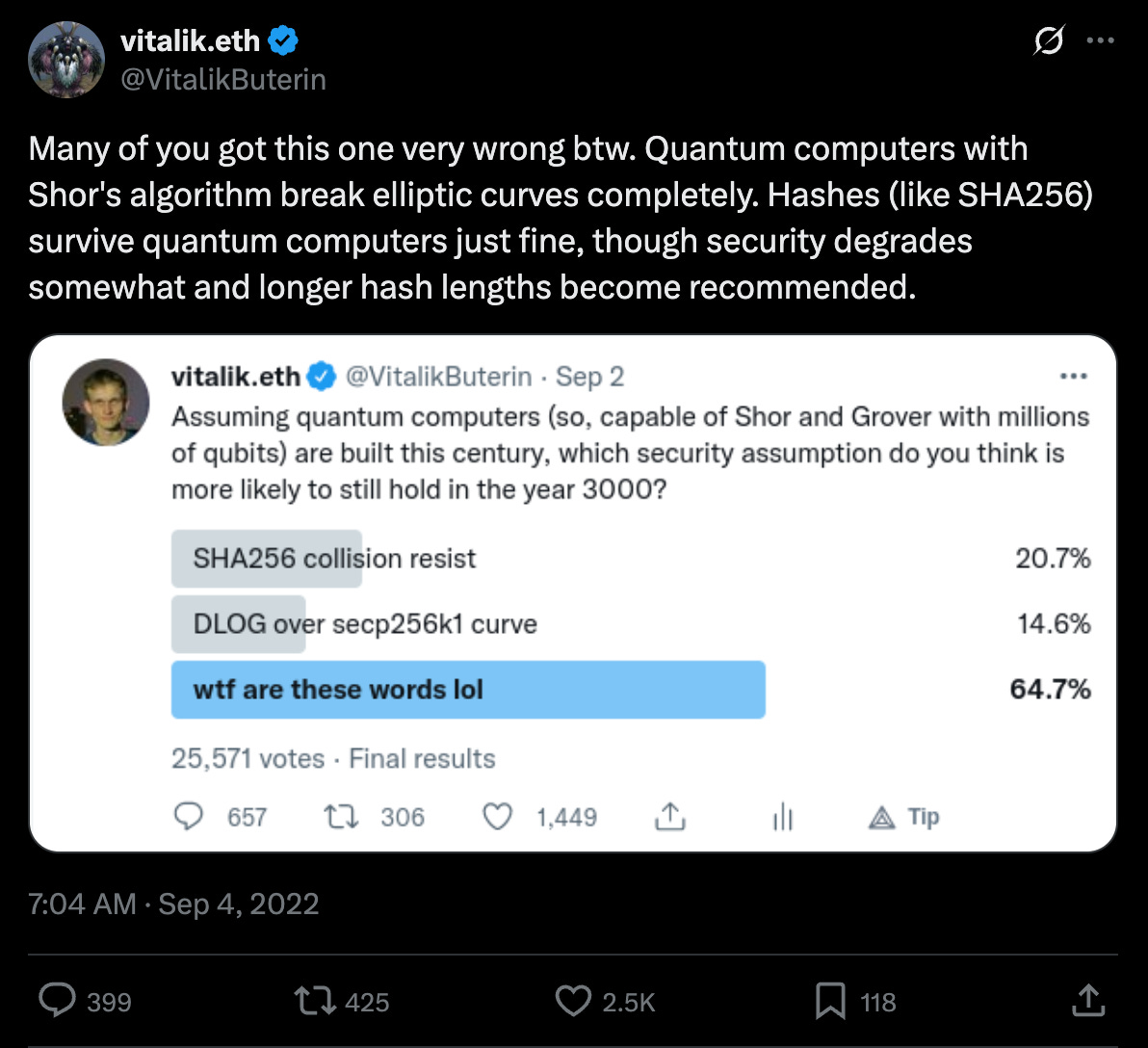
Throughout my career in blockchain, researchers have considered quantum computing as a threat to the security primitives of blockchain.
Many blockchains, such as Ethereum and Bitcoin, enable users to securely interact with the chain through elliptic curve cryptography, including ECDSA. As later explained in the article, quantum computing can easily break elliptic curve cryptography, allowing hackers to steal user funds.
Top researchers, including Vitalik Buterin, the founder of Ethereum, and Dan Boneh, a cryptography and computer security professor at Stanford University, have voiced concerns:


How ECDSA is used on the blockchain
Many popular blockchains, including Ethereum and Ethereum-compatible (or Ethereum Virtual Machine-based) chains, Bitcoin, Polkadot, and others, integrate ECDSA as a core backend component to enable users to use the chain securely.
The Elliptic Curve Digital Signature Algorithm (ECDSA) is used to generate keys, authenticate, sign, and verify messages on many popular blockchains. Any major security vulnerability in ECDSA would render users unable to use the blockchain securely, potentially resulting in the loss of funds.
Generate keys
A blockchain is an immutable ledger, similar to a one-table SQL database, that cannot be altered or erased.
To send data to a blockchain, a user needs to generate a wallet, which comes with a pair of keys that serve as their entry point into the blockchain and the primary method for storing their cryptocurrency on the blockchain. When a user creates a wallet, the client software or the software that connects and interacts with the blockchain:
Generates an ECDSA private key that the user should only know (think of a private key like your bank account details). As mentioned in the upcoming sections, an ECDSA private key can be used to generate a signature that proves wallet ownership or confirms the sending of data or a transaction.
Derives a public key from the private key [1]
Hashes the public key into a blockchain address that can be shared widely (think of a blockchain address as your Venmo or PayPal ID) [2]
Compromising ECDSA could allow hackers to control a user’s wallet completely without the user’s knowledge.
Authenticate and sign
Once a user has a wallet, they can send data or make a transaction to the blockchain. For example, they can send Bitcoin to another address.
To make a proposed transaction, the user needs to provide the inputs (which address they are spending from), outputs (which address the funds are going to), an amount, and a nonce (a unique, randomly-generated number). The nonce is critical as it makes the transaction unique, even if the user intends to send the same amount of Bitcoin to the same address in the future.
Then, to confirm the transaction, the user approves the proposed transaction on their wallet, signing the hash computed from the proposed transaction and generating an ECDSA signature that is added to the final transaction object.
Compromising ECDSA would enable hackers to send transactions without the user’s permission.
Verify transactions
A proposed transaction is then sent to a node or a device that is permitted to send transactions to a specified blockchain.
When a node receives a transaction, it parses the data and pulls out the sender’s public key and the ECDSA signature. Then it re-hashes the transaction data or raw data and runs elliptic curve math to check that the signature matches the hash and the sender’s public key.
If everything checks out, the transaction is considered authentic and moves into the mempool, where it can later be included in a block by miners or validators. If it does not pass verification, the node rejects it right away [3].
As explained later, quantum computing could enable hackers to forge ECDSA signatures and send transactions without user permission, making it impossible for nodes to distinguish between fraudulent and legitimate transactions.
How ECDSA is currently secure and how quantum computing can break ECDSA
It is nearly impossible to guess an ECDSA private key or signature using standard computing.
There are still various attack vectors that users can face, but hackers guessing the private details of their wallet or creating a valid signature that can approve sending of funds to another wallet are currently not among them (given a correctly done implementation of ECDSA).
Quantum computing, which has the potential to surpass the combined computing power of all existing computers, could change that.
Securing private keys
An ECDSA private key is a large integer in an astronomically extensive range, making it impossible to guess. On many popular blockchains, it is 256-bit binary digits, meaning that it is 256 digits long with a total of 2²⁵⁶ unique possibilities.
Probability of finding a key with funds
You can pick any 256-bit number, and most 256-bit numbers are valid private keys. But choosing a random one that matches somebody else’s key had a very low probability.
Currently, there are 1.068 million active addresses on Ethereum. For simplicity, let’s assume that each address is mapped to one private key.
(If you want to learn more about which addresses are actually mapped to a private key, check out this forum post on OpenZeppelin.)
1.068 million / 2²⁵⁶ = Your chances are 9.223428 x 10^-72 or 1 in 10^-72 or 0.00000000000000000000000000000000000000000000000000000000000000000000000009223428 in finding a private key attached to funds.
Let’s assume that everyone in the world has an Ethereum private key. Your chances are still very low:
8.248 billion / 2²⁵⁶ = Your chances are 7.1231118 x 10^-68 or 1 in 10^−68 or 0.000000000000000000000000000000000000000000000000000000000000000071231118 in finding a private key attached to funds.
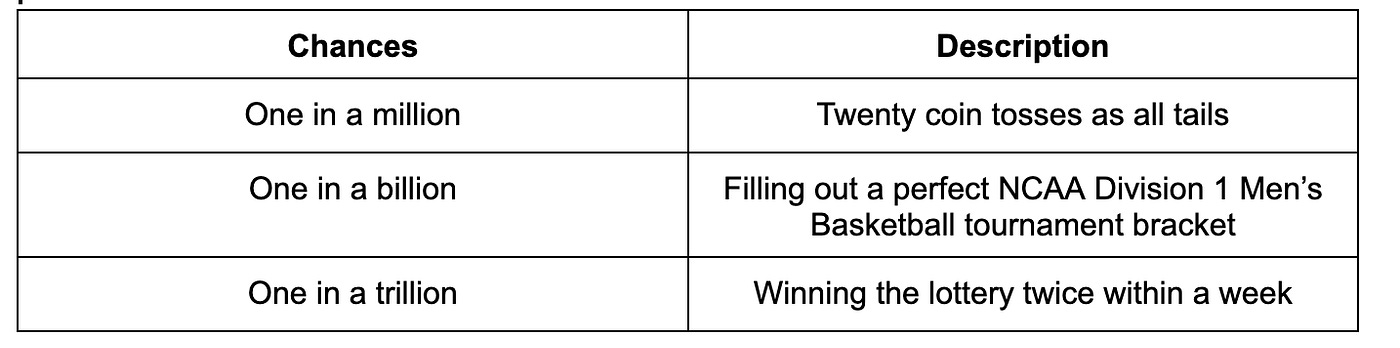
You are more than 60 times more likely to win the lottery twice within a week than randomly finding an active Ethereum private key.
Storage and time constraints to check every single private key
Iterating through all possible private keys also requires an astronomically significant amount of storage and time.
It is currently impossible to store all possible private keys. A 256-bit private key is 32 bytes in size. It would take approximately 1.447 × 10⁶⁷ standard 256-GB laptops, which would require a massive amount of space, to store 2^256 private keys.
((2^256) * (32 bytes)) / (256 GB) = 1.447 × 10^67 laptopsOn the other hand, a small quantum computer can potentially store all private keys, as it already contains the state of all the world’s hard drives combined. Quantum computer storage is based on bits or qubits, which, unlike conventional computers, can handle multidimensional storage. The largest quantum computer consists of 6,100 qubits trapped in a total width of only one millimeter. Only 100 qubits are required to surpass the storage capabilities of all of the world’s hard drives combined [5].

Even if you can store all private keys on a standard computer, it would take a significant amount of time to iterate and check each private key.
Let’s assume that a standard computer can check one trillion private keys per second. It would take 3.67 x 10⁵⁷ or 36700000000000000000000000000000000000000000000000000000000000 years to iterate through all possible private keys.
(2^256) / (1*10^12 * 86400 seconds * 365 days) = 3.67 × 10^57 yearsOn the other hand, it would take much less time on an advanced quantum computer that could be developed in the future. Researchers simulated that it would require 317,000,000 qubits to iterate through all possible private keys in an hour [6]. It is still unlikely that an existing quantum computer can iterate through all private keys, as the largest existing quantum computer is only 6,100 qubits. However, as the field progresses, the likelihood that a quantum computer can do so within a reasonable timeframe is high.
Generating a private key based on a public key
Generating a private key using a public key is also tricky.
ECDSA is based on Elliptic Curve Cryptography (ECC), a cryptographic algorithm that generates keys based on the properties of the algebraic structure of elliptic curves.
The private key is a randomly computed 256-bit integer. The public key is generated from the private key using elliptic curve multiplication, as represented here at a high level:
Randomly compute an integer d in the interval [1,n — 1]
Calculate Q = dG
The public key computed is Q, and the private key is d
To find the private key using the public key, you must compute G, which is nearly impossible [4]. You can’t simply use division d = Q/G to find the private key, as Elliptic Curve Cryptography is based on geometry.
This problem, known as the Elliptic Curve Discrete Logarithm Problem, could be solved within hours using a quantum computer. Researchers broke the 256-bit elliptic curve discrete logarithm in nine hours using 126,000 cat qubits, a special qubit designed for greater stability and resistance to errors [7].
Conclusion
The security of blockchains depends on the strength of the cryptography that underpins them.
While ECDSA is currently secure, the rise of quantum computing poses a significant threat to its long-term viability. Quantum computing could lead hackers to control user wallets and make fraudulent, unauthorized transactions.
Users utilize blockchain technology because they trust that it can provide secure storage for their cryptocurrency and can handle tamper-proof data. With the compromise of ECDSA and other cryptographic algorithms, blockchains will need to implement new quantum-proof algorithms or render themselves useless.
Sources
[1] What is the Elliptic Curve Digital Signature Algorithm? — ECDSA Signatures, https://www.cyfrin.io/blog/elliptic-curve-digital-signature-algorithm-and-signatures
[2] The Math Behind the Bitcoin Blockchain: Part Two, https://www.elliptic.co/blockchain-basics/the-math-behind-the-bitcoin-blockchain-part-two/lipiurnlipaged_flagship3_profile_view_base_post_detailspdg5lpbttmgkpqwxrxeepw
[3] ECDSA Explained: The Backbone of Digital Signature Security, https://www.nervos.org/knowledge-base/understanding_ECDSA_(explainCKBot)
[4] Performance and Security of ECDSA, http://koclab.cs.ucsb.edu/teaching/ecc/project/2015Projects/Levy.pdf
[5] A primer of quantum computing storage and memory, https://www.techtarget.com/searchstorage/tip/A-primer-on-quantum-computing-storage-and-memory
[6] The impact of hardware specifications on reaching quantum advantage in the fault-tolerant regime, https://pubs.aip.org/avs/aqs/article/4/1/013801/2835275/The-impact-of-hardware-specifications-on-reaching
[7] Computing 256-bit elliptic curve logarithm in 9 hours with 126,133 CAT qubits, https://alice-bob.com/blog/computing-256-bit-elliptic-curve-logarithm-in-9-hours-with-126133-cat-qubits/#:~:text=are%20realized%2C%20and%20that%20a,days%20using%20350%2C000%20cat%20qubits.



